很简单的一个插件,现在支持汉化Sublime Text2,Sublime Text3。全部系统Win64、Win32,Linux64,Linux32,OSX等,可以随意来回切换简体中文、繁体中文、日语、英语,无需重启SublimeText。
迁移wordpress博文到octopress
导言
本来我没有把wordpress迁移过来的打算,就像我发现Movable Type生成的页面无比的快,依然还是比较喜欢Wordpress。这里不像展开讨论PHP和Perl、Ruby甚至Python的优缺点比较,总之存在就是合理的。网上你可以轻易搜索得到100个提供PHP空间的免费服务器,而那些提供其他语言的一般都会提供PHP,就连谷歌也都开始试验PHP了,总之这是市场的需求。PHP是看上去没有那种学院气派,没有一总令人眼前一亮的内在哲学美。PHP出生就像是一个下乡的乡巴佬,看起来那么的不和谐,各种不一致,简直像一门自然语言,但是它是人造的。关于PHP的指责可以看这里。
问题
好了回到本文的正题上来,我的博客采用了三种语言的方式,提供了中文、日语、英文。因此字符集是比较大的,在我这里算是一个特殊情况。博客运行有两三年了(早期是用的免费主机,然后也不知道备份,严重丢失过一次,应该是09或者10年开始的),博文有210+篇,这样的话要尽量减少人工参与的程度,当然个别特殊的还是需要处理下的,比如有的标题中我用了引号或者*/?等符号的,这种个别的问题rake generate时报错直接手工修改就好。另外代码中如果有{ {双左大括号出现,那么也会出错,解决办法便是加一个空格隔开。
解决工具:
我已经git push到了这里
命令:
|
效果:
 以及本博客.
以及本博客.
发布流程
废话不多说,简单的说明下。需要注意的两个命令:
|
可以开着然后用MarkdownPad 2修改,octopress会随时监视文件修改然后的自动重新生成,打开网页便可以预览.而且可以省去delploy前的generate。效果如下图: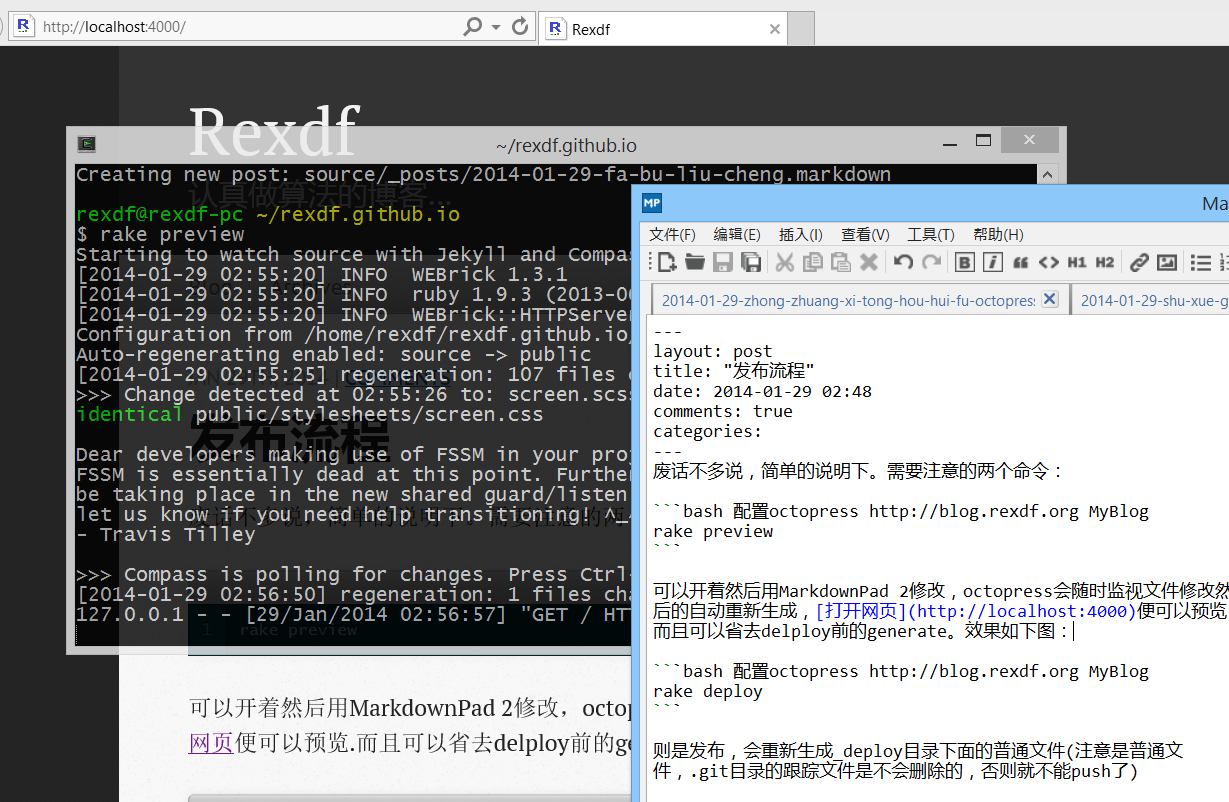
然后发布
|
则是发布,会重新生成_deploy目录下面的普通文件(注意是普通文件,.git目录的跟踪文件是不会删除的,否则就不能push了)
|
数学公式测试2
大家都喜欢用 $E=mc^2$ 举例子,但是我不是很理解。
这个公式 $\cos 2\theta = \cos^2 \theta - \sin^2 \theta = 2 \cos^2 \theta - 1$ 少年可还记得?
插入方程组(注意多行公式结尾\需要打成\,可能是因为markdown会自动转义第一个\): $$\begin{aligned} \dot{x} & = \sigma(y-x) \ \dot{y} & = \rho x - y - xz \ \dot{z} & = -\beta z + xy \end{aligned} $$
插入矩阵(同上):
来个复杂点的(注意有的公式开头不会自动识别,用$$包围):
最后来个牛逼的吧,薛定谔方程,大学物理就记得这个了:
洛伦兹公式
柯西-施瓦茨不等式
叉积公式
n次实验k次成功的概率
拉马努金恒等式
Rogers–Ramanujan恒等式
麦克斯韦方程组
最后,当呈现整页看上去很棒的例子后,把数学公式与文本混合1同样重要。这个表达式 $\sqrt{3x-1}+(1+x)^2$ 是一个行内等式例子。正如你所见,MathJax中这种等式也可以试用的很好,而不必变更行间距。
重装系统后恢复octopress
起因
好久没有更新这个blog了,最近突然又想写点东西,然而加上SSD后重新装了系统,这次想git clone代码下来,而不是push force来处理,顺便熟悉下git的分支管理。
cygwin环境
由于重新安装过了cygwin,这次安装完全按照感觉来装的,虽然装了gcc的三大平台版本(gnu-gcc,gcc-mingw,gcc-cygwin)以及gdb和cmake这些常用的编译工具,然而却忽视了gnu-make,这就是一个悲剧。在git clone了imathis的octopress的源码之后发现怎么也安装不上RedCloth这下可是悲剧了。然后一番搜索发现似乎没有RedCloth安装出问题的,而最近cygwin更新也非常频繁,gcc都升级到4.8.2了,最近的文章进谷歌索引也比较慢,再说人家解决问题也不一定会写文章。抱着比较悲观的情绪,无意中点开了一份Octopress入门安装过程,然后对照其cygwin的安装选项发现了我没有安装make,没有安装make!!这只要在任何一个项目中执行以下就会发现的,基本上是不可以编译任何项目了!!
解决过程很简单安装gnu-make即可。然后就是下面的恢复过程了
恢复octopress
|
这样便把source分支clone下来了。
|
接下去应该是要输入博客仓库地址。(当然如果提示rake版本问题,直接修改Gemfile里面的0.9为10.1即可。或者使用bundle exec rake setup_github_pages也可以。)
|
最后则是删除生成的_deploy,克隆master分支
|
这样便恢复了本地的代码。
Zoj-3753
Simple Equation
Time Limit: 2 Seconds Memory Limit: 65536 KB
There are many Equations. Some are difficult to solve, for example: an xn + an-1 xn-1 + .. + a0 = 0. In this problem, you are given a simple equation: AX + BY = XY. To simplify the problem, here A, B, X, Y are positive integers. Your task is to find the solution (X, Y) of this equation where X is not less than M. If there are multiple solutions, you should choose the solution with the minimal X + Y. If there are still ties, you should choose the solution with the minimal X.
Input
There are multiple test cases (about 3000). For each test case: There is only one line contains three integers A, B (1 <= A, B <= 10 ^ 9) and M (1 <= M <= 10 ^ 18).
Output
For each test case, output X and Y. If there is no valid solution, output “No answer” instead.
Sample Input
1 1 2
1 1 3
3 4 8
3 4 9
Sample Output
2 2
No answer
8 6
10 5
Author: LIANG, Mingqiang Source: ZOJ Monthly, January 2014
题意解释:
这题还是比较好做的,我当做最简单题来做的。很容易对原式变形得到:这样问题就变形了对\(A \times B\)这个数进行因式分解即可。A、B范围是\(10^9\),这样分别对A、B因式分解只需要考虑小于\(10^5\)的素数测试就好了。另外估算一下:① \( 2 \times 3 \times 5 \times 7 \times 11 \times 13 \times \cdots \times 29 = 6,469,693,230 > 1 \times 10^9\) ,这里最多10个素数;② \( 2^{60}=1,152,921,504,606,846,976 > 1 \times 10^{18}\)即指数和最大不超过60。因此这个计算过程是可以暴力进行的。也就是说对\(A \times B\)的每个因子进行一次枚举即可。设\(A \times B\)的一个因子是\(x_0\),那么就这样暴力下去即可以解决了。
代码
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
using namespace std;
//分解质因数
//prime_factor()传入n, 返回不同质因数的个数
//f存放质因数,nf存放对应质因数的个数
//先调用initprime(),其中第二个initprime()更快
#define PSIZE (95592+5)
long long plist[PSIZE];
int pcount=0;
int prime(long n){
int i;
if ((n!=2&&!(n%2))||(n!=3&&!(n%3))||(n!=5&&!(n%5))||(n!=7&&!(n%7)))
return 0;
for (i=0;plist[i]*plist[i]<=n;++i)
if (!(n%plist[i]))
return 0;
return n>1;
}
void initprime(){
int i;
for (plist[pcount++]=2,i=3;i<100000;++i)
if (prime(i))
plist[pcount++]=i;
}
int prime_factor(long n, long * f, int *nf) {
int cnt = 0;
long n2 = sqrt((double)n);
for(int i = 0; n > 1 && plist[i] <= n2; ++i)
if (n % plist[i] == 0) {
for (nf[cnt] = 0; n % plist[i] == 0; ++nf[cnt], n /= plist[i]);
f[cnt++] = plist[i];
}
if (n > 1) nf[cnt] = 1, f[cnt++] = n;
return cnt;
}
long long mod_pow(long p,int k){
long long ret=1,q=p;
while(k){
if(k&1)ret*=q;
k>>=1;
q=q*q;
}
return ret;
}
long A,B,mid;
long long M;
long a[15],b[15],c[15];
int an[15],bn[15],cn[15];
int acnt,bcnt,ccnt;
long long ans1,ans2;
int v[15];
void dfs(int cnt){
if(cnt==ccnt){
long long test=1,t1,t2;
for(int i=0;i<ccnt;i++){
test*=mod_pow(c[i],v[i]);
}
t1=B+test;
t2=1LL*A*B/test+A;
if(t1>=M){
if(-1==ans1 || t1+t2<ans1+ans2 || (t1+t2==ans1+ans2 && t1<ans1))ans1=t1,ans2=t2;
}
return;
}
for(int i=0;i<=cn[cnt];i++){//第cnt+1个素数可以取值0...cnt
v[cnt]=i;
dfs(cnt+1);
}
}
int main(){
initprime();
//cout<<pcount<<endl;
while(~scanf("%ld%ld%lld",&A,&B,&M)){
//mid=sqrt(A)*sqrt(B)+0.6;
acnt=prime_factor(A,a,an);
bcnt=prime_factor(B,b,bn);
ccnt=0;
for(int i=0,j=0;i<acnt || j<bcnt;){
if((i<acnt && j<bcnt && a[i]<b[j]) || (j==bcnt && i<acnt)){
c[ccnt]=a[i];
cn[ccnt]=an[i];
ccnt++;
i++;
}
else if((i<acnt && j<bcnt && a[i]>b[j]) || (i==acnt && j<bcnt)){
c[ccnt]=b[j];
cn[ccnt]=bn[j];
ccnt++;
j++;
}
else{
c[ccnt]=a[i];
cn[ccnt]=an[i]+bn[j];
ccnt++;
i++;
j++;
}
}
ans1=-1;
dfs(0);
if(-1==ans1)printf("No answer\n");
else printf("%lld %lld\n",ans1,ans2);
}
return 0;
}
Zoj-3752
The Three Guys
Time Limit: 2 Seconds Memory Limit: 65536 KB Special Judge
Recent days, a joke spread out among Chinese social networks. “If Yao Ming, Guo Jingming and He Jiong lying on the ground, can they form a triangle?” Some netizens think that it is impossible to form a triangle since Yao Ming is a basketball giant, while Guo Jingming and He Jiong are artists with short statures. But another group of netizens came out and claim: “Yes, they can!” Someone even has presented a sketch to prove their theory:

There are three guys in somewhere of the world. They have learned of this idea and want to try it out by themselves. Given you the height of the three guys, please find out the maximum area of triangle they can form. The height consists of two parts: the upper part of body Ui and the lower part of body Li.
Input
There are multiple test cases (about 3000). For each test case: There are three lines. Each line consists of two integers Ui and Li (1 <= Ui, Li <= 150) indicates the height of two parts of the i-th guy.
Output
For each test case, output the maximum area of triangle they can form. Any solution with a relative or absolute error of at most 1e-9 will be accepted.
Sample Input
10 10
20 20
30 30
Sample Output
600.000000000000
Author: JIANG, Kai Source: ZOJ Monthly, January 2014
题意解释:
额,不想具体多说,转换一下,三段可以折叠的木棍,组成面积最大的三角形。由于很久没有做过zoj了,昨天想去看看zoj的月赛,结果悲催的没做出来。赛后调试发现double就可以过,int就不行,这才发现zoj的int是16位整数,而long才是32位整数,不像不像cf的int直接就是32位的,刚刚开始想错了边长是\((150 \times 2)=300\),而不是我以为的150,故计算过程是超过32位int了的,顺便说一句zoj的long和long long是一样的都是64位整数,不想其他的long和int一样,不过最好不要使用long,因为按照标准int<=long<=long long即可以,那么long取4或者8都是合理的。解法很多,如果思维足够缜密,那么用if是可以写出来的,3!2^320=4320种情况,但是真的用if应该小于这么多情况。另外就是排列组合的生成了,可以递归也可以while写。
代码
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
using namespace std;
inline double area_triangle(int a,int b,int c){
long q=1L*(a+b+c)*(a+b-c)*(a+c-b)*(b+c-a);//!!3*150^4=1,518,750,000溢出Int!!! ZOJ int:16 long:32
return sqrt(q)/4.0;
}
inline int is_tri(int a,int b,int c){
return a+b>c && a+c>b && b+c>a;
}
int main(){
int a[4][2],b[6],sum;
int p1[3]={0,1,2};
int p2[3][2]={ {0,1},{0,1},{0,1}};
int a1,a2,a3;
double ans,tmp;
while(~scanf("%d%d %d%d %d%d",&a[0][0],&a[0][1],&a[1][0],&a[1][1],&a[2][0],&a[2][1])){
ans=0;
sum=0;
for(int i=0;i<6;i++){
sum+=a[i>>1][i&1];
}
p1[0]=0,p1[1]=1,p1[2]=2;
do{
//printf("#%d %d %d\n",p1[0],p1[1],p1[2]);
p2[0][0]=0,p2[0][1]=1;
do{
p2[1][0]=0,p2[1][1]=1;
do{
p2[2][0]=0,p2[2][1]=1;
do{
for(int i=0;i<6;i++){
b[i]=a[p1[i>>1]][p2[p1[i>>1]][i&1]];
}
for(int i=0;i<4;i++){
for(int j=i+1;j<5;j++){
for(int k=j+1;k<6;k++){
a2=0,a3=0;
for(int l=i;l<j;l++){
a2+=b[l];
}
for(int l=j;l<k;l++){
a3+=b[l];
}
a1=sum-a2-a3;
if(is_tri(a1,a2,a3)){
tmp=area_triangle(a1,a2,a3);
if(tmp>ans)ans=tmp;
}
}
}
}
}while(next_permutation(p2[2],p2[2]+2)); //前后摆放2种
}while(next_permutation(p2[1],p2[1]+2)); //前后摆放2种
}while(next_permutation(p2[0],p2[0]+2)); //前后摆放2种
}while(next_permutation(p1,p1+3)); //三个人下标排序有3!=6种情况
printf("%.10lf\n",ans);
}
return 0;
}
重装系统如何删除cygwin文件夹
cygwin最近更新频繁,在win8.1上面使用起来兼容性基本没啥问题,应该来说win7+上面都是兼容的挺好的。不过我最近添加了个SSD,然后重装系统到SSD上面,想保留使用了段时间的Ubuntu系统,没有格式化硬盘,用Ubuntu-Live-CD的U盘把MBR写到了SSD上面,然后做成了完全保留原来的老Win8.1系统的样子,cygwin这样的东西就没有必要装到ssd里面了,然而就发现老的cygwin没法删除了。办法不是没有的,点右键修改权限是可以的,但是实际操作起来就发现,所有者是可以递归进行的,而权限是没法递归的,实际结果就是怎么也删不掉,2G左右的文件夹大小,都是些几k的文件,一个个改权限显然不现实,解决办法如下: 1.Win+X然后按A,打开管理员控制台; 2.进入cygwin所在的目录输入
takeown /F cygwin /R
icacls cygwin /T /grant 用户名:F
rd /s /q Cygwin
大约5分钟等待,然后文件夹就消失了。 文件夹安全选项中烦人的数字账户
for /d %i in ("opencv") do (
ICACLS "%i" /setowner "%username%" /t /c /q
ICACLS "%i" /reset /t /c /q
)
如果在批处理中则用%%i替换%i即可,以上的%i单个%是命令行直接敲的。
茄子快传
挂Q小记
写在最前:这篇文字是描述的我的一个没有成功的代码,鉴于某些原因成功的代码就不公布了。能写出来的自然容易,100来行代码就可以搞定,而且由于手机QQ版本繁多,方法也是万千的。不管是截封包,还是逆向源代码,基本上都是可以取得一定收获的。对于这种问题,我一贯作风是只保证刚刚满足自己的需求即可,也懒得作深入探究。 鉴于最近TX的QQ升级规则最重要的一条改成了连续6小时手机QQ,而电脑加速则最多只有0.5天。我尚不清楚3GQQ算不算手机QQ,但是我实践中是不算的,然而登录记录上看属于手机QQ的,那么应该是我的每2小时更换一次登录IP的缘故吧。现在很容易的可以实现3GQQ,手机QQ似乎调试的时候遇到了一些问题。当然应该是腾讯版本比较繁多,其中一个版本遇到了问题,也就是我前面那篇文章提到的。
$s=new socketc("58.60.12.177",14000);
while($row = mysql_fetch_array($result))
{
$s->socket();
$r=rand(200,999);
$var_msg="VER=1.4&CON=1&CMD=Login&SEQ=".$r."UIN=".$row['qq_number']."&PS=".strtoupper(md5($row['qq_pw']))."&M5=1&LG=0&LC=812822641C978097&GD=5MWX2PF3FOVGTP6B&CKE=\r\n";
echo $row['qq_number']."<br/>";
$var_retu = ($s->sendmsg($var_msg)) or die("Empty receive!\n");
/*$s->sendmsg("VER=1.4&CON=1&CMD=Login&SEQ=112255&UIN=316926989&PS=61E9315B47B2851C910091FB5AF495C2&M5=1&LG=0&LC=812822641C978097&GD=5MWX2PF3FOVGTP6B&CKE=\r\n");*/
print_r($var_retu);
$vars_retu = explode('&', $var_retu);
if(strpos($vars_retu[1],"VERIFYCODE"))
{
$vars_vc = explode('=',$vars_retu[7]);
$vercode = @pack("H*",$vars_vc[1]);
echo "<form action='ajax_mobile.php' method='post'>";
echo "<img src='data:image/png;base64,". base64_encode($vercode)."'/>";
echo "<input type='hidden' name='_qqcode' value='".$row['qq_number']."'> </input>";
echo "<input type='text' name='_vercode'></input><input type='submit' value='验证'></input><br/>";
echo "</form>";
}
echo $var_msg."<hr/>";
$s->close();
}
嗯,这段代码是以52挂Q为蓝本的,本来我调试的时候已经写好了应答代码,只是不知道从什么时候开始好像突然被疼迅加入黑名单了,反正怎么调试疼迅的应答都是空的,我收到的都是空对象。但是奇葩的是我用的另一个代码就可以使用的。现在部署的是另一套手机QQ的代码,这里就不贴出来了。上面这个代码我本地在无法重现,也就懒得取消数据库依赖以及服务器部署测试了。(起初大约一两个小时都是可用的,可以看到验证码,然后我还尝试着训练我验证码识别库,可以突然就不可以了,也换过几个不同的IP,socket://58.60.12.177:14000,socket://211.136.236.88:14000,http://tqq.tencent.com:8000,http://mconn.tencent.com:14000,http://kconn.tencent.com:21001,我试验过前面两个,后面的懒得实验,因为我已经可以满足需求也没必要这么折腾)。
叹陈晓旭
不小心看到了87版《红楼梦》中林黛玉扮演者陈晓旭女士相关的事情。本来只是在看艺术人生-红楼梦再回首节目视频,可是“可恶”的相关视频硬生生推荐看了几个关于陈晓旭女士追悼以及张莉女士回国后的红楼再回首,一时间感慨万千。 首先来感叹下陈晓旭女士居然41岁仙逝,应该说《红楼梦》的演出对其性格有较大稳固,按说王夫林导演选人是很注重性格天然重合的。古代佛教在人们日常生活地位较重,这在《红楼梦》书中融入的比较深,如妙玉和高鄂版本宝玉、惜春出家都是有推崇佛教的意味,容易产生皈依佛门是崇高追求,是人生完美的感觉。写到这里,大约能佐证为啥马克思在中国行得通(某些意义上)。 当然,个人信仰是自由的,大部分民主国家应该都如是。宗教,应该都具有较为长久的历史。宗教需要从信众心里产生信仰,于是会在宗教发展历史进程中依据当时科技水平,对信众问题进行解答,并借此发展其理论。一些宗教都是尚古的,也就是“圣人”都是久远时代的,这是为了确立信众身份的卑微,然后再开始灌输其核心价值观理论、以及宗教规则。当然,如果剥去唯心主义信仰和唯心主义崇拜对人心理负面影响。宗教,还起着部分正面的社会道德的作用。对于佛教,入世出世、因果报应、积善成德等,应该每一个中国人心中都是有一份认同感的,至少是熟悉这些内容的。 陈晓旭女士应该说从看到的视频上,她是坦然面对死亡的,死前皈依佛门,死后成立基金会。而且对于她自身来说,她应该也以为这个过程很完美。但是对于她的父母、丈夫、朋友以及广大粉丝观众们,则是令人惋惜、悔恨的。 虽然以前知道林黛玉扮演者好像癌症去世了这么一回事,但是今天网上一搜,相关文章非常之多,很大一部分可以归结为以下关键词:固执大意、延误治疗、迷信中医、误信庸医、信佛、基金会空壳、各界悼词。而其本人居然可以在好友之间保密那么久,简直不可思议,自然又是其性格原因。 07年那时候应该在高一高二,这使我想起老师天天念叨的一句话来:性格即命运!不过第一次看87版红楼梦,也才是这个月的事,某天偶然原因一口气看了十来集,发觉非常有意思,然后就开始找脂评本的《红楼梦》和周汝昌汇校红楼梦,逛贴吧,而到今天我依然压着每天半集一集地看,才过二十多集,实在不忍心看完!当然也是上周才知道有陈晓旭这个人的。